LBA (long branch
attraction)
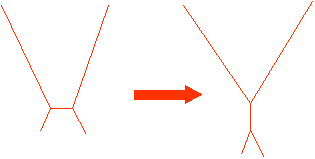
Na prvním obrázku je skutečný strom čtyř taxonů. Větve mají
různou délku, větve vedoucí k A a B jsou delší, třeba proto, že v těchto liniích
je vyšší mutační
rychlost. Joseph Felsenstein upozornil na to, že pokud poměr délek dlouhých větví k ostatním
větvím na stromu
překročí určitou hranici bude z hlediska maximální parsimonie nejlepší strom, kde budou dlouhé
větve příbuzné.
Zjednodušeně si to můžeme představit tak, že během evoluce těchto taxonů bude…
Je potřeba zdůraznit, že LBA nemizí pokud se zvýší počet dat.
Metody náchylné
na LBA totiž způsobuje inkonzisteci metody. To znamená, že když se počet dat blíží
nekonečnu, metoda
s pravděpodobnosti blížící se 1 vybere špatnou topologii.
ML a Distance nejsou inkozistentní protože korigují
mnohonásobné substituce. Platí to však pouze pokud jsou distance určeny
správně a je použit evoluční model odpovídající skutečnosti. Volba modelu
a parametrů je
problém.
p a q = pravděpodobnost, že na větvi dojde k změně znaku z
jednoho stavu na druhý. Závisí exponenciálně na čase a mutační rychlosti =
délka větve.
Felsensteinova zóna = takový poměr p a q při kterém se metoda
chová inkozistentně.
S nekonečným počtem dat vybere s pravděpodobností 1 špatnou topologii
(hypotézu). Čím více stavů, tím je menší – proteiny.
Parsimonie je ikonzistentní, protože nekoriguje vícenásobné
substituce. Ve F zóně je vyšší pravděpodobnost vzniku konvergentní mutace
na dlouhých
větvích (p2) nez informativní
mutace
na prostřední větvi (q).
ML a Distance nejsou inkozistentní protože korigují
mnohonásobné substituce. Platí to však pouze pokud jsou distance určeny
správně a je použit evoluční model odpovídající skutečnosti. Volba modelu
a parametrů je problém.

Pravděpodobnost vzniku
konvergentní mutace na dvou dlouhých větvích je vyšší než pravděpodobnost vzniku informativní mutace na
větvi, která je odděluje.
Skutečný strom
Nejparsimonnější strom
A
A
D
C
B
D
C
B