Constitutive models are integrated using explicit adaptive integration scheme with local substepping.
The constitutive model forms an ordinary differential equation of the form
The equation is for finite time step size 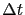 solved using the Runge-Kutta method. Solutions that correspond to the
second- and third- orded accuracy of Taylor series expansion are given by
solved using the Runge-Kutta method. Solutions that correspond to the
second- and third- orded accuracy of Taylor series expansion are given by
where
The accuracy of the solution is estimated following Fehlberg as the difference between the second- and third- order solutions. The time step size
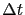 is accepted, if
is accepted, if
where 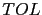 is a prescribed error tollerance. If the step-size
is a prescribed error tollerance. If the step-size 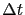 is accepted,
is accepted,
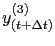 is considered as a solution for the given
time step and the new time step size
is considered as a solution for the given
time step and the new time step size
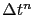 is estimated according to Hull
is estimated according to Hull
If the step-size 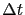 is not accepted, the step is re-computed with new time step size
is not accepted, the step is re-computed with new time step size
In the case the prescribed minimum time step size or the prescribed maximum number of time substeps is reached, the finite element program is asked
to reject the current step and to decrease the size of the global time step.
David Masin
2011-02-07
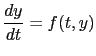
![]() solved using the Runge-Kutta method. Solutions that correspond to the
second- and third- orded accuracy of Taylor series expansion are given by
solved using the Runge-Kutta method. Solutions that correspond to the
second- and third- orded accuracy of Taylor series expansion are given by
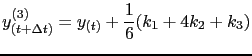
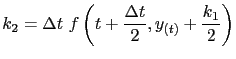
![]() is accepted, if
is accepted, if
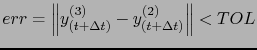
![$\displaystyle \Delta t^n={\rm min}\left[4\Delta t, 0.9 \Delta t \left(\frac{TOL}{err}\right)^{1/3}\right]$](img13.png)
![$\displaystyle \Delta t^n={\rm max}\left[\frac{\Delta t}{4}, 0.9 \Delta t \left(\frac{TOL}{err}\right)^{1/3}\right]$](img14.png)