(version September 2001)
Aims and basic features
Some simulations
Further information
The model is able to capture the following processes:
"What I cannot create, I do not understand''
(R. D. Feynmann's last writing on his blackboard, Jan. 1988)
I wrote this simulator in order to understand better mechanisms behind the spatiotemporal structure of clonal plants forming the mountain grasslands I have been studying with my colleagues in the past decade. It got a lot of inspiration from the work I did with Richard Law and Ulf Dieckmann on individual-based modelling of these systems (this simulator is a kind of an extension of that work which did not include architectural constraints and was more directed toward theoretical research). Primary questions we wanted to investigate were:
Later it turned out it can be used for a variety of more theoretical studies (see our 2002 paper in Evolutionary Ecology with Jun-ichirou Suzuki) and that we found some information to parameterise it to represent very different systems (clonal and non-clonal trees, experimental communities etc.)
And it produces nice structures.
Below are few examples of different clonal structures (for some other
ones, and discussion of the uses of the model, see also our Freising
talk with Radka Wildová).
A rhizome growing in an erratic way
This is a plant that tends to grow by primary rhizomes with high s.d. of growth angle (perhaps Polygonum cuspidatum as we did some preliminary modelling of it with Katerina Bimova; I think in Japan it looks rather differently!).

This is after 40 steps. (NB. The plantlet at the other side of the plot is just a visual demonstration what a toroidal boundary is doing. Notice also some density dependent mortality here.)
The parameter values are as follows:
no_isr = 0, no_rsr = 0, mode_to_clonal = 0, criter_to_clonal = 0.000, how_many_clonal = 1.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.2000, K_clonal = 1.000, init_size = 1.0000, diam_a = 0.0000, diam_b = 0.0000, accum = 5.0000, stp_accum = 0, cv_accum = 0.0000, res_retained = 1.0000, res_stored = 0.5000, alpha = 0.5000, beta = 0.1000, dens_indep = 0.0000, sharing_range = 0, prop_shared = 0.5000, p_trans_node = 0.5000, p_trans_tip = 0.5000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0000, fr_res_tip = 0.7000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 1, r = 0.01000, cv_r = 0.30000, sd_angle = 30.0000, nodes_to_die = 100, nodes_alive = 100, br_allowed = 1, prob_term_br = 1.0000, bra_angle = 30.0000, bra_orient = 0, length_primary = 1.0000, fr_n_primary = 1.0000, nodes_primary = 1, fr_p_primary = 1.0000, sleeping_bud = 0.1000, prob_lateral = 0.0000, lifespan = 950, cv_life = 0.0000, neighb_size = 0.05000, deg_asym= 1.00000, fire = 0.00000.
(Don't worry about the high number of parameters. Most of them are switching off processes that do not take place anyway).
A plant with circular tussocks
This is an example of circular tussock growth with no resprouting in
the centre (after 40 steps):
This is the parameter file:
no_isr = 1, no_rsr = 0, mode_to_clonal = 0, criter_to_clonal = 10.000, how_many_clonal = 15.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.2000, K_clonal = 1.000, init_size = 1.0000, diam_a = 0.0000, diam_b = 0.0000, accum = 10.0000, stp_accum = 0, cv_accum = 0.0000, res_retained = 1.0000, res_stored = 0.5000, alpha = 0.5000, beta = 0.0500, dens_indep = 0.0000, sharing_range = 0, prop_shared = 0.5000, p_trans_node = 0.5000, p_trans_tip = 0.5000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0000, fr_res_tip = 0.7000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 1, r = 0.00500, cv_r = 0.30000, sd_angle = 3.0000, nodes_to_die = 100, nodes_alive = 100, br_allowed = 1, prob_term_br = 1.0000, bra_angle = 5.0000, bra_orient = 0, length_primary = 5.0000, fr_n_primary = 0.0000, nodes_primary = 5, fr_p_primary = 0.0000, sleeping_bud = 0.1000, prob_lateral = 0.0000, lifespan = 950, cv_life = 0.0000, neighb_size = 0.05000, deg_asym= 1.00000, fire = 0.00000.
If some potential for resprouting in the centre is added, it is going to look like that (40 steps; notice that some density dependent mortality occurred at the side branches):

This is the parameter file:
no_isr = 1, no_rsr = 0, mode_to_clonal = 0, criter_to_clonal = 10.000, how_many_clonal = 15.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.2000, K_clonal = 1.000, init_size = 1.0000, diam_a = 0.0000, diam_b = 0.0000, accum = 10.0000, stp_accum = 0, cv_accum = 0.0000, res_retained = 1.0000, res_stored = 0.5000, alpha = 0.5000, beta = 0.0500, dens_indep = 0.0000, sharing_range = 0, prop_shared = 0.5000, p_trans_node = 0.5000, p_trans_tip = 0.5000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0000, fr_res_tip = 0.7000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 1, r = 0.00500, cv_r = 0.30000, sd_angle = 3.0000, nodes_to_die = 100, nodes_alive = 100, br_allowed = 1, prob_term_br = 1.0000, bra_angle = 5.0000, bra_orient = 0, length_primary = 5.0000, fr_n_primary = 0.0000, nodes_primary = 5, fr_p_primary = 0.0000, sleeping_bud = 0.5000, prob_lateral = 0.0200, lifespan = 950, cv_life = 0.0000, neighb_size = 0.05000, deg_asym= 1.00000, fire = 0.00000
If the plant gets the ability to form a long rhizomes from time to time, it changes its shape as to get the following (40 steps again; the scale is different now):

This is the parameter file:
no_isr = 0, no_rsr = 0, mode_to_clonal = 0, criter_to_clonal = 10.000, how_many_clonal = 15.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.2000, K_clonal = 1.000, init_size = 1.0000, diam_a = 0.0000, diam_b = 0.0000, accum = 10.0000, stp_accum = 0, cv_accum = 0.0000, res_retained = 1.0000, res_stored = 0.5000, alpha = 0.5000, beta = 0.0500, dens_indep = 0.0000, sharing_range = 0, prop_shared = 0.5000, p_trans_node = 0.5000, p_trans_tip = 0.5000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0000, fr_res_tip = 0.7000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 1, r = 0.00500, cv_r = 0.30000, sd_angle = 3.0000, nodes_to_die = 100, nodes_alive = 100, br_allowed = 1, prob_term_br = 1.0000, bra_angle = 5.0000, bra_orient = 0, length_primary = 5.0000, fr_n_primary = 0.0200, nodes_primary = 5, fr_p_primary = 0.0200, sleeping_bud = 0.5000, prob_lateral = 0.0200, lifespan = 950, cv_life = 0.0000, neighb_size = 0.05000, deg_asym= 1.00000, fire = 0.00000
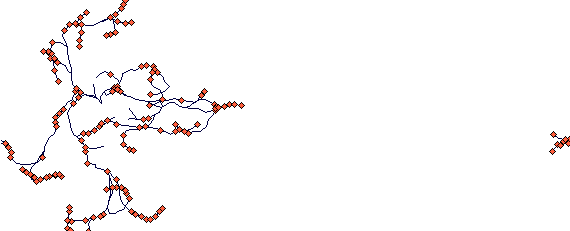
Another plant with two rhizome types
This is a plant that has two rhizome types: long primary rhizomes that exploit environment and short rhizomes that build up a tussock.
This is again after 40 steps. The parameter values are:
no_isr = 0, no_rsr = 0, mode_to_clonal = 0, criter_to_clonal = 0.000, how_many_clonal = 1.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.2000, K_clonal = 1.000, init_size = 1.0000, diam_a = 0.0000, diam_b = 0.0000, accum = 5.0000, stp_accum = 0, cv_accum = 0.0000, res_retained = 1.0000, res_stored = 0.5000, alpha = 0.5000, beta = 0.0500, dens_indep = 0.0000, sharing_range = 0, prop_shared = 0.5000, p_trans_node = 0.5000, p_trans_tip = 0.5000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0000, fr_res_tip = 0.7000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 1, r = 0.00500, cv_r = 0.30000, sd_angle = 5.0000, nodes_to_die = 100, nodes_alive = 100, br_allowed = 1, prob_term_br = 1.0000, bra_angle = 50.0000, bra_orient = 0, length_primary = 5.0000, fr_n_primary = 0.0200, nodes_primary = 5, fr_p_primary = 0.0200, sleeping_bud = 0.1000, prob_lateral = 0.0000, lifespan = 950, cv_life = 0.0000, neighb_size = 0.05000, deg_asym= 1.00000, fire = 0.00000.
A creation based on this simulation is to be found here.
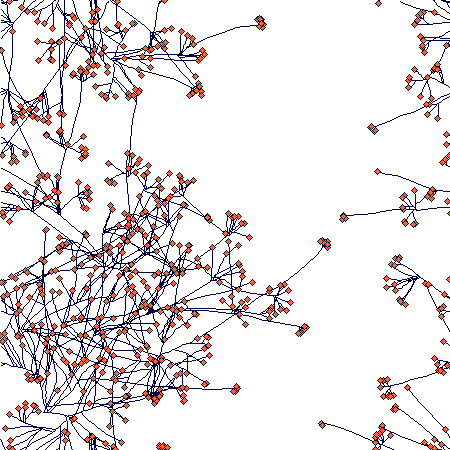
For the same parameter setting, this is the density-dependent increase in density over 100 steps:
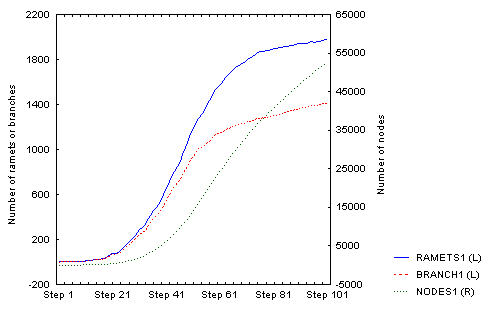
There is an obvious (but not full - I was lazy to wait) slowing down of the increase in number of ramets; number of nodes will follow, but with a lag that corersponds to the value of nodes_to_die (= 100), so it may take some further 100 steps or so. The spatial structure then looks like this:
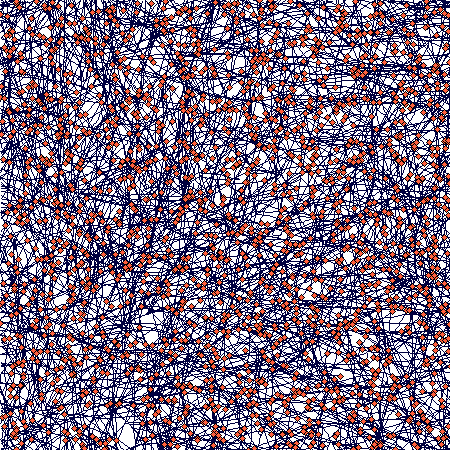
If you zoom in, the following picture emerges:

It shows how tussocks are mixed one with the other (a result of translocation being switched off), but still some tussock structure is distinguishable.
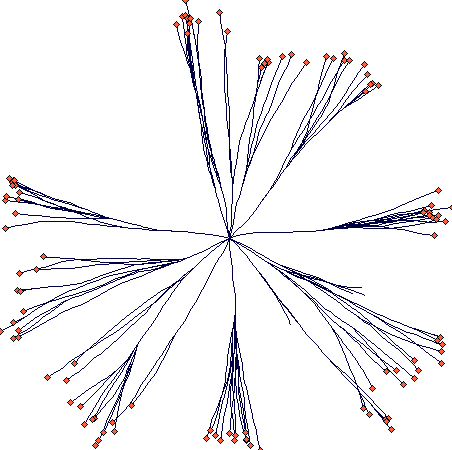
Density dependence and branching rate
This an exploration how the branching rate will change with increasing density. It is not as simple as the above example seems to indicate. This shows a plant with only one type of branching and nodes staying alive for 50 steps. After 50 steps, it looked like this:

Until then the number of branches and nodes were increasing. After that, they began to decrease and oscillated at a slightly lower value. Number of ramets stayed approximately the same (this is the direct outcome of density-dependence: only ramets compete directly). This is the whole time course:
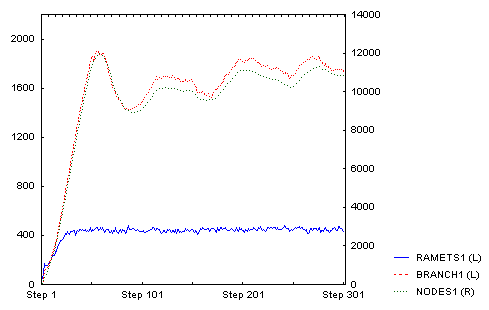
And this is how it looked after 300 steps (there is clearly a lot of density dependent mortality of tips of individual branches):

This is the parameter setting: no_isr = 50.000, no_rsr = 0.000, mode_to_clonal = 0, criter_to_clonal = 0.000, how_many_clonal = 1.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.2000, K_clonal = 1.000, init_size = 1.0000, diam_a = 0.0000, diam_b = 0.0000, accum = 10.0000, stp_accum = 0, cv_accum = 0.0000, res_retained = 1.0000, res_stored = 0.5000, alpha = 0.5000, beta = 0.3000, dens_indep = 0.0000, sharing_range = 0, prop_shared = 0.5000, p_trans_node = 0.5000, p_trans_tip = 0.5000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0000, fr_res_tip = 0.7000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 1, r = 0.01000, cv_r = 0.30000, sd_angle = 8.0000, nodes_to_die = 50, nodes_alive = 50, br_allowed = 1, prob_term_br = 1.0000, bra_angle = 40.0000, bra_orient = 0, length_primary = 5.0000, fr_n_primary = 0.0000, nodes_primary = 5, fr_p_primary = 0.0000, sleeping_bud = 0.5000, prob_lateral = 0.0500, lifespan = 950, cv_life = 0.0000, neighb_size = 0.05000, deg_asym= 1.00000, fire = 0.00000
Effects of individual parameters on competitive performance
Now two completely identical species are run together, starting with 25 plants each. These plants were completely identical, differing only in the value of a single parameter, which was changed for the plant species 1. (This is the value that is plotted on the x-axis in teh plots below.) After 100 steps, the proportion of the species 1 out of the total number of ramets was calculated (that is the y-value in the graphs below). It enables to test how much one parameter affects competitive performance of a clonal species.
NB. These results, in a more condensed form, are in our 2002 Evolutionary
Ecology paper with Jun-ichirou Suzuki.
The experiment was done with three plant 'types':
B - basic
S - capable of activating older sleeping nodes
V - variable sizes of ramets
For the parameter values of these plants, look here.
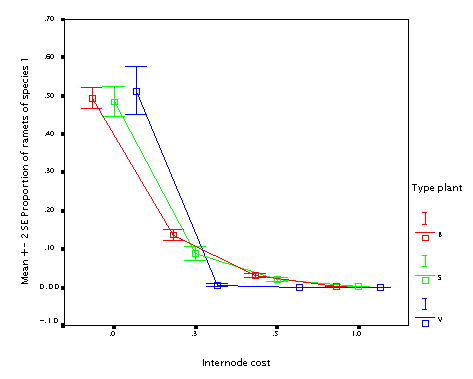
This is the effect of varying internode cost. Quite expectable. Plants building more costly internodes lose, no matter what type of the plant.
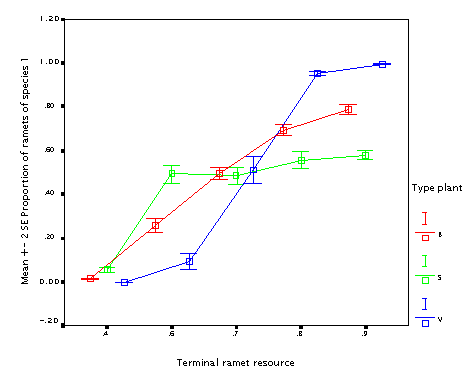
This is the effect of varying fraction of the resource available at the mother node put into the daughter node (fr_tip). Well, if you have an offspring, it is always better to put more resource into it. But if your offspring is just as big as you are (B and S plants) it is not as useful.
This is the effect of internode length (r). The longer internodes, the better! (In particular if the plant size varies.) This seems to contradict the fact that guerrilla plants tend to be weaker competitors.
NB. but this simulation works under the assumption that all other things are equal; longer internodes than change the proportion between interspecific and intraspecific competition; since there is no translocation, the more compact plants tend to outcomete its own ramets. As a result, differences make a lot of difference when internodes are short; if they are long (longer than the neighbourhood size), the difference does not matter. Neighbourhood size was 0.05 in this case; since thisvalues is the radius, it is just the double of this value when the effect disappears.)
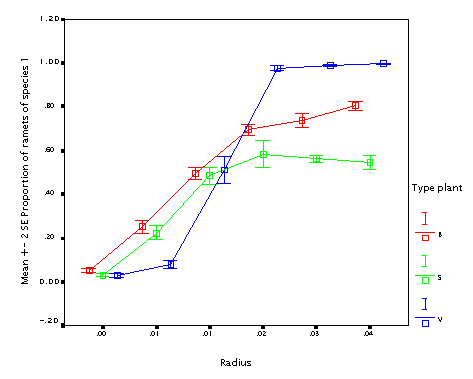
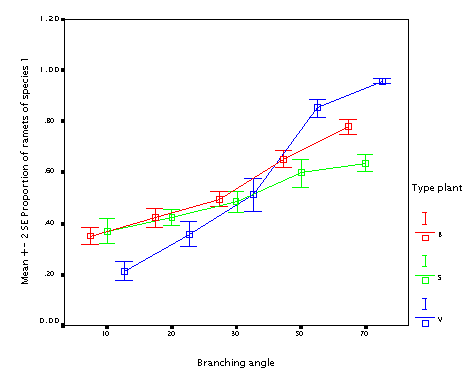
This is the effect of branching angle. Again, the bigger branching angle, the better, with the same argument as for the internode length.
Listing of parameter values for the three plant types (differences against the B plant are marked in bold and red).
Plant B:
no_isr = 25, no_rsr = 0, mode_to_clonal = 0, criter_to_clonal = 0.000, how_many_clonal = 1.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.2000, K_clonal = 1.000, init_size = 1.0000, diam_a = 0.0000, diam_b = 0.0000, accum = 3.5000, stp_accum = 0, cv_accum = 0.0000, res_retained = 1.0000, res_stored = 0.5000, alpha = 0.5000, beta = 0.100, dens_indep = 0.0000, sharing_range = 0, prop_shared = 0.5000, p_trans_node = 0.5000, p_trans_tip = 0.5000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0000, fr_res_tip = 0.7000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 1, r = 0.0100, cv_r = 0.10000, sd_angle = 10.0000, nodes_to_die = 20, nodes_alive = 20, br_allowed = 3, prob_term_br = 1.0000, bra_angle = 30.0000, bra_orient = 0, length_primary = 5.0000, fr_n_primary = 0.0000, nodes_primary = 5, fr_p_primary = 0.0000, sleeping_bud = 0.0000, prob_lateral = 0.0000, lifespan = 950, cv_life = 0.0000, neighb_size = 0.05000, deg_asym= 1.00000, fire = 0.00000
Plant S:
no_isr = 25, no_rsr = 0, mode_to_clonal = 0, criter_to_clonal = 0.000, how_many_clonal = 1.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.2000, K_clonal = 1.000, init_size = 1.0000, diam_a = 0.0000, diam_b = 0.0000, accum = 3.5000, stp_accum = 0, cv_accum = 0.0000, res_retained = 1.0000, res_stored = 0.5000, alpha = 0.5000, beta = 0.100, dens_indep = 0.0000, sharing_range = 0, prop_shared = 0.5000, p_trans_node = 0.5000, p_trans_tip = 0.5000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0000, fr_res_tip = 0.7000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 1, r = 0.0100, cv_r = 0.10000, sd_angle = 10.0000, nodes_to_die = 20, nodes_alive = 20, br_allowed = 3, prob_term_br = 1.0000, bra_angle = 30.0000, bra_orient = 0, length_primary = 5.0000, fr_n_primary = 0.0000, nodes_primary = 5, fr_p_primary = 0.0000, sleeping_bud = 0.0500, prob_lateral = 0.0500, lifespan = 950, cv_life = 0.0000, neighb_size = 0.05000, deg_asym= 1.00000, fire = 0.00000
Plant V:
no_isr = 25, no_rsr = 0, mode_to_clonal = 0, criter_to_clonal = 0.000, how_many_clonal = 1.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.8000, K_clonal = 1.000, init_size = 0.1000, diam_a = 0.0000, diam_b = 0.0000, accum = 3.5000, stp_accum = 0, cv_accum = 0.0000, res_retained = 1.0000, res_stored = 0.5000, alpha = 0.5000, beta = 0.100, dens_indep = 0.0000, sharing_range = 0, prop_shared = 0.5000, p_trans_node = 0.5000, p_trans_tip = 0.5000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0000, fr_res_tip = 0.7000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 1, r = 0.0100, cv_r = 0.10000, sd_angle = 10.0000, nodes_to_die = 20, nodes_alive = 20, br_allowed = 3, prob_term_br = 1.0000, bra_angle = 30.0000, bra_orient = 0, length_primary = 5.0000, fr_n_primary = 0.0000, nodes_primary = 5, fr_p_primary = 0.0000, sleeping_bud = 0.0000, prob_lateral = 0.0000, lifespan = 950, cv_life = 0.0000, neighb_size = 0.05000, deg_asym= 1.00000, fire = 0.00000
With Radka Wildová we attempted to get the simulator parameterized for some real species. Radka took rather extensive morphological and growth data of several calcareous fen species collected by Deborah Goldberg and her students (Chad Hershock, Martina Petru and Radka herself). In addition, Deborah has a wonderful set of experiments that could be used to calibrate the model.
Since the model has many parameters, the parameterizing was not very easy and for some parameters we have no idea of their true values. (And there is no translocation in the model as we have no parameters for that.) Still the result was not too bad - some species yielded soon, some other less easily (Radka is writing a paper on that).
Here is a sample simulation of two species (each initially planted in four individuals): Carex sterilis (the more clumped species) and Carex lasiocarpa (the more loose species). Only one quarter of the simulation plane shown (except for the last image). (The parameter settings are here.) This is just a try with many parameters being still a sort of guestimates identical for both species.
Day 200
(Eight plant - four of each species have been planted. Carex lasiocarpa plants are in the left side of the plane. Carex sterilis is beginning to form tussocks while Carex lasiocarpa forms more extensive rhizome systems, but the difference between the two is not yet very obvious.)
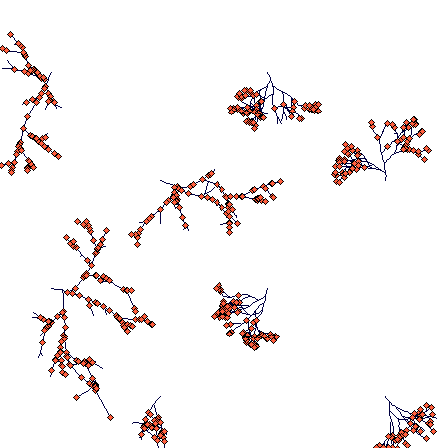
Day 300
(notice the slowly fragmenting clumped structure of Carex sterilis and rhizomatous Carex lasiocarpa, which managed to travel much large distances. One of its rhizomes is heading directly to a Carex sterilis tussock.)
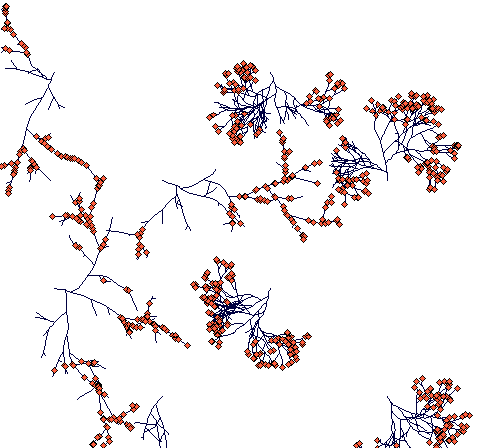
Day 400
(most of the ramets and terminal nodes of Carex lasiocarpa are dead because of competition. A few rhizomes are still alive, one of them thriving in an open space in between two Carex sterilis tussocks.)
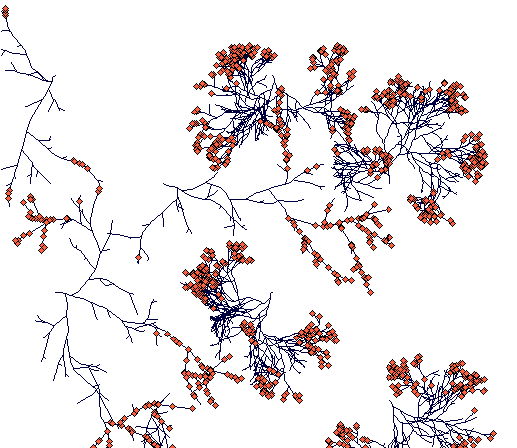
Day 500
(one of the Carex lasiocarpa rhizomes is finding its way through tussocks of Carex sterilis. The other rhizome hit a Carex sterilis clump and died. Carex sterilis has fragmented into compact but separated clumps of ramets.)
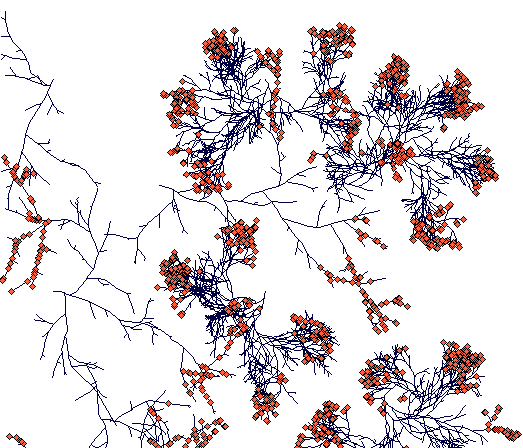
Day 700
(while Carex sterilis is closing the space, the surviving rhizome of Carex lasiocarpa managed to escape.)
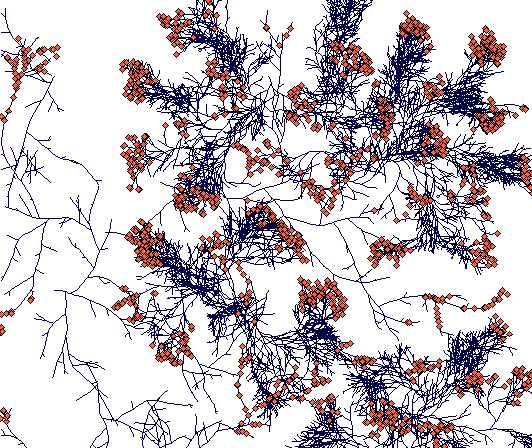
Day 900
(This is a zoomed out figure showing the whole simulation plane with toroidal boundaries - plants crossing the boundary just appear on the opposite side. Notice the compact tussock of Carex sterilis and rhizomatous structures of Carex lasiocarpa. The C. lasiocarpa rhizome that found its way through Carex sterilis tussocks now faces interaction with another Carex lasiocarpa plant. But I did not leave it run that long, and the result is thus unknown to the world.)

Parameter settings (This is a slightly different version of the model from that shown above, hence the differences in the parameter list)
Parameters that differ between species are shown in red.
Carex lasiocarpa
step_isr = 0, no_isr = 4.000, no_rsr = 0.000, mode_to_clonal = 0, criter_to_clonal = 0.000, how_many_clonal = 1.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.0180, K_clonal = 1.280, init_size = 0.1080, diam_a = 0.0000, diam_b = 0.0000, accum = 3.0000, stp_accum = 0, cv_accum = 0.0000, feedb_max = 1.0000, feedb_exp = 0.1000, feedb_dist = 0.1000, feedb_node = 0, res_retained = 1.0000, res_stored = 0.5000, alpha = 2.0000, beta = 0.0050, dens_indep = 0.0000, sharing_range = 0, prop_shared = 1.0000, p_trans_node = 1.0000, p_trans_tip = 1.0000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0100, fr_res_tip = 0.2000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 10, r = 0.00540, cv_r = 0.77000, sd_angle = 10.0000, nodes_to_die = 1000, nodes_alive = 1000, br_allowed = 3, prob_term_br = 1.0000, bra_angle = 50.0000, bra_orient = 2, length_primary = 1.0000, prop_primary = 1.0000, length_long = 4.3000, fr_n_long = 0.0000, nodes_long = 11, fr_p_long = 0.0000, sleeping_bud = 0.0000, prob_lateral = 0.0000, lifespan = 16, cv_life = 0.1000, neighb_size = 0.05500, deg_asym= 1.00000, fire = 0.00000
Carex sterilis
step_isr = 0, no_isr = 4.000, no_rsr = 0.000, mode_to_clonal = 0, criter_to_clonal = 0.000, how_many_clonal = 1.000, start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 1.000, r_clonal = 0.0140, K_clonal = 0.730, init_size = 0.0720, diam_a = 0.0000, diam_b = 0.0000, accum = 3.0000, stp_accum = 0, cv_accum = 0.0000, feedb_max = 1.0000, feedb_exp = 0.1000, feedb_dist = 0.1000, feedb_node = 0, res_retained = 1.0000, res_stored = 0.5000, alpha = 2.0000, beta = 0.0050, dens_indep = 0.0000, sharing_range = 0, prop_shared = 1.0000, p_trans_node = 1.0000, p_trans_tip = 1.0000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost = 0.0010, fr_res_tip = 0.2000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast = 5, r = 0.00280, cv_r = 0.37000, sd_angle = 10.0000, nodes_to_die = 1000, nodes_alive = 1000, br_allowed = 4, prob_term_br = 1.0000, bra_angle = 40.0000, bra_orient = 2, length_primary = 1.0000, prop_primary = 1.0000, length_long = 4.3000, fr_n_long = 0.0000, nodes_long = 11, fr_p_long = 0.0000, sleeping_bud = 0.0000, prob_lateral = 0.0000, lifespan = 20, cv_life = 0.1000, neighb_size = 0.05500, deg_asym= 1.00000, fire = 0.00000
Just for fun, I tested whether the model will show self-thinning if clonal growth is switched off and plants are of variable size (hardly would have sense for ramets of identical size....). It then becomes just a very simple model of growth and density change of a community of non-clonal plants. It produced (over 200 steps, starting with 300 'seedlings) this:
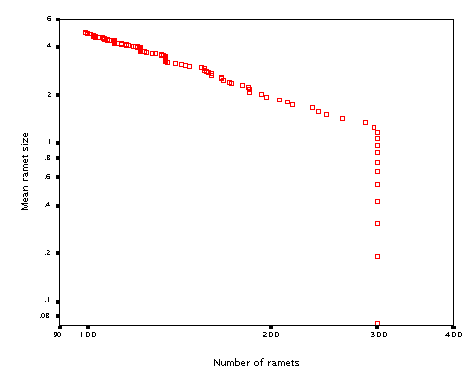
The line has a slope of 1.28. Some experimentation showed that the slope of the line (quite expectedly) strongly depends on the 'inverse' allometric parameter diam_b (the exponent that links radius of the zone of influence to the ramet biomass).
Parameter setting for this run: no_isr = 300.000, no_rsr = 0.000,
mode_to_clonal = 0, criter_to_clonal = 1000.000, how_many_clonal = 1.000,
start_orient = 0, r_nonclonal = 0.0500, K_nonclonal = 5.000, r_clonal =
0.0500, K_clonal = 5.000, init_size = 0.0100, diam_a = 0.1000, diam_b =
0.2000, accum = 5.0000, stp_accum = 0, cv_accum = 0.0000, res_retained
= 1.0000, res_stored = 0.5000, alpha = 2.0000, beta = 3.0000, dens_indep
= 0.0000, sharing_range = 0, prop_shared = 1.0000, p_trans_node = 1.0000,
p_trans_tip = 1.0000, p_basipet = 0.5000, cost_trans = 0.0000, internode_cost
= 0.0000, fr_res_tip = 0.7000, flost_res = 0.8000, fsurv = 0.5000, steps_per_plast
= 1, r = 0.02000, cv_r = 0.10000, sd_angle = 5.0000, nodes_to_die = 50,
nodes_alive = 50, br_allowed = 1, prob_term_br = 1.0000, bra_angle = 50.0000,
bra_orient = 0, length_primary = 1.0000, fr_n_primary = 1.0000, nodes_primary
= 1, fr_p_primary = 1.0000, sleeping_bud = 0.0000, prob_lateral = 0.0000,
lifespan = 950, cv_life = 0.0000, neighb_size = 0.09400, deg_asym= 1.00000,
fire = 0.00000.
I thank Takuya
Kubo for a lot of inspiration on websites on simulation modelling! I also
would like to say that functions of the simulator owe a lot to Radka Wildová
and Jun-ichirou Suzuki. I would have never started working on it without Richard
Law and Ulf Dieckmann.