Regresní techniky v Excelu

Měříme závislost proměnné y na jedné nebo více nezávisle proměnných. Hodnoty nezávisle proměnných nastavíme pevně. Naměřené hodnoty závisle proměnné vykazují určité odchylky – kolísání (obvykle na nich mají velký podíl experimentální chyby) kolem neznámé střední hodnoty.

Budeme studovat závislost proměnné y na jedné nezávisle proměnné x. Provedeme n měření. Získáme tak body (x_i,y_i), i=1,2,…n. Předpokládejme, že naše měřená závislost je matematicky formulována známým zákonem - rovnicí y=f(x). Funkci f budeme nazývat regresní funkce.

Regresní funkci proložíme naměřenými daty tak, abychom naším prokladem zmíněné kolísání dat minimalizovali. Tím zároveň určíme odhad neznámých parametrů regresní funkce. Jinak řečeno, cílem regrese je určit takové hodnoty parametrů regresní funkce, aby tato funkce co nejlépe prokládala zadaná data.

Excel již obsahuje nástroje, které tyto hodnoty parametrů, pro regresní funkce lineární vzhledem k parametrům, počítají. Používá k tomu samozřejmě metodu nejmenších čtverců. Po získání odhadů regresních parametrů lze z regresní funkce vypočítat, po zadání hodnoty nezávisle proměnné x, odpovídající odhad závisle proměnné y. Popsanému výpočtu říkáme predikce.

Funkce LinRegrese()

• Y je vektor o n prvcích, kde n je počet měření. Obsahuje hodnoty jednotlivých měření y_i závisle proměnné y. Budeme jej zadávat jako vektor sloupcový. Tedy i-tý řádek tohoto vektoru obsahuje hodnotu závisle proměnné pro i-té měření.
• X je matice o n řádcích a m sloupcích, kde m je počet regresorů. V každém sloupci obsahuje hodnoty příslušného regresoru. I-tý řádek této matice obsahuje hodnoty regresorů pro i-té měření f_k (x_i), k=1,...,m. Pokud bychom jednotlivá měření zadávali ve sloupcích, role řádků a sloupců se zamění.
• B – určuje, zda závislost obsahuje absolutní člen (vynechán, nebo PRAVDA obsahuje, NEPRAVDA či nula – neobsahuje absolutní člen).
• Stat – je-li PRAVDA, poskytuje funkce další statistické charakteristiky regrese, je-li NEPRAVDA, nebo bez zadání – funkce je neposkytuje. Hodnotu tohoto parametru nebudeme zpravidla zadávat.

Pokud žádáme od funkce LinRegrese() jen výpočet odhadu parametrů b_j, je jejím výsledkem jednořádková matice o počtu sloupců, který je roven počtu těchto parametrů. Nutno zdůraznit, že pořadí získaných parametrů je opačné, než pořadí sloupců s hodnotami příslušných regresorů v argumentu X. Absolutní člen b₀ je vždy poslední. Počítáme-li další statistické charakteristiky regrese (Stat=TRUE), zadáme pro výslednou matici funkce LinRegrese() obdélník o pěti řádcích a počtu sloupců, který je roven počtu hledaných parametrů.

Příklady regresních funkcí.

1. Regresní funkce y=b₀+b₁ x (regresní přímka) je lineární vzhledem k neznámým parametrům b₀,b₁, pro regresor f₁(x) platí f₁(x)=x. Výchozími daty pro regresi bude tabulka o dvou sloupcích. V prvním bude n hodnot nezávisle proměnné (argument X), ve druhém n hodnot závisle proměnné (argument Y). Výsledná matice parametrů funkce LinRegrese() bude obsahovat po řadě parametry b₁,b₀.
2. Regresní funkce y=b₀+b₁ x+ b₂ x² (regresní parabola) je lineární vzhledem k neznámým parametrům b₀,b₁,b₂, pro regresor f₁(x) platí f₁(x)=x, pro regresor f₂ (x) platí f₂ (x)=x². Výchozími daty pro regresi bude tabulka (matice) o třech sloupcích a n řádcích. V prvním sloupci budou hodnoty nezávisle proměnné, ve druhém hodnoty čtverců nezávisle proměnné (tyto dva sloupce tvoří argument X) a ve třetím budou hodnoty závisle proměnné (argument Y). Výsledná matice parametrů funkce LinRegrese() bude obsahovat po řadě parametry b₂,b₁, b₀. Změníme-li pořadí sloupců v argumentu X, změní se pořadí získaných parametrů na b₁,b₂, b₀.
3. Regresní funkce y=b₀+b₁ x₁+ b₂ x₂ je lineární vzhledem k neznámým parametrům b₀,b₁,b₂. Je to funkce dvou proměnných x₁ a x₂, které jsou zároveň regresory. Výchozími daty pro regresi bude tabulka o třech sloupcích a n řádcích. V prvním sloupci budou hodnoty nezávisle proměnné x₁, ve druhém hodnoty nezávisle proměnné x₂ (tyto dva sloupce tvoří argument X) a ve třetím bude n hodnot závisle proměnné (argument Y). Výsledná matice parametrů funkce LinRegrese() bude obsahovat po řadě parametry b₂,b₁, b₀. Změníme-li pořadí sloupců v argumentu X, změní se pořadí získaných parametrů na b₁,b₂, b₀.
4. Regresní funkce y=b₁ .e^(b₂.x)+ b₃ .e^(b₄.x) není lineární vzhledem k parametrům b₂ a b₄. Proto nelze k výpočtu hodnot jejich parametrů použít funkce LinRegrese().

Regrese obecnou přímkou y=b₀+b₁x

• Funkce Slope(Y, X) – poskytuje směrnici b₁ regresní přímky.
• Funkce Intercept(Y, X) – navrací y-ovou souřadnici b₀ průsečíku přímky s osou y.
• Maticová funkce LinRegrese(Y, X, B, Stat) poskytuje řádkovou matici parametrů b₁ a b₀ (nezadáme-li parametr Stat).

X je vektor hodnot nezávisle proměnné x.

Y je vektor obsahující odpovídající naměřené hodnoty závisle proměnné y.

Hodnotu B nezadáváme.

Hodnotu Stat zadáme jen v tom případě, požadujeme-li statistické charakteristiky regrese.

Pracovní postup

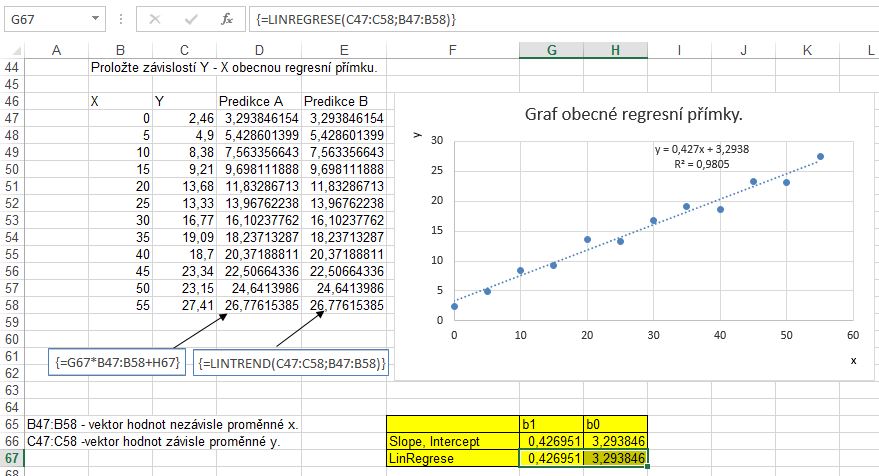
• Vyznačíme zdrojová data X,Y (následující obrázek B47:C58).
• Sestrojíme z nich bodový graf.
• Z kontextové nabídky libovolného bodu grafu volíme příkaz Přidat spojnici trendu. Objeví se okno „Formát spojnice trendu“. V něm klepneme na volbu Lineární a dále zaškrtneme volbu Zobrazit rovnici v grafu a volitelně volbu Zobrazit hodnotu spolehlivosti R².
• Pro výpočet regresních parametrů funkcí LinRegrese() vyznačíme dvě sousední buňky v řádku (G67:H67). Tlačítkem f_x zvolíme funkci LinRegrese(). Zadáme argumenty Y a X. Zadání ukončíme Ctrl+Shift+Enter. Parametr b₁ je první zleva, b₀ druhý. Příslušný vzorec vidíme na řádku vzorců.
• Hodnoty predikce počítáme z rovnice regresní funkce, či maticovou funkcí LinTrend(). Stačí zadat její první dva argumenty Y, X.

Regrese přímkou procházející počátkem y=b₁x

• Funkce Slope() a Intercept() nelze v tomto případě použít.
• Maticová funkce LinRegrese(Y, X, B, Stat) poskytuje řádkovou matici parametrů b₁ a b₀=0.

X je vektor hodnot nezávisle proměnné x.

Y je vektor obsahující odpovídající naměřené hodnoty závisle proměnné y.

Hodnotu B zadáváme rovnou nule.

Hodnotu Stat zadáme jen v tom případě, pokud bychom požadovali statistické charakteristiky regrese.

Pracovní postup

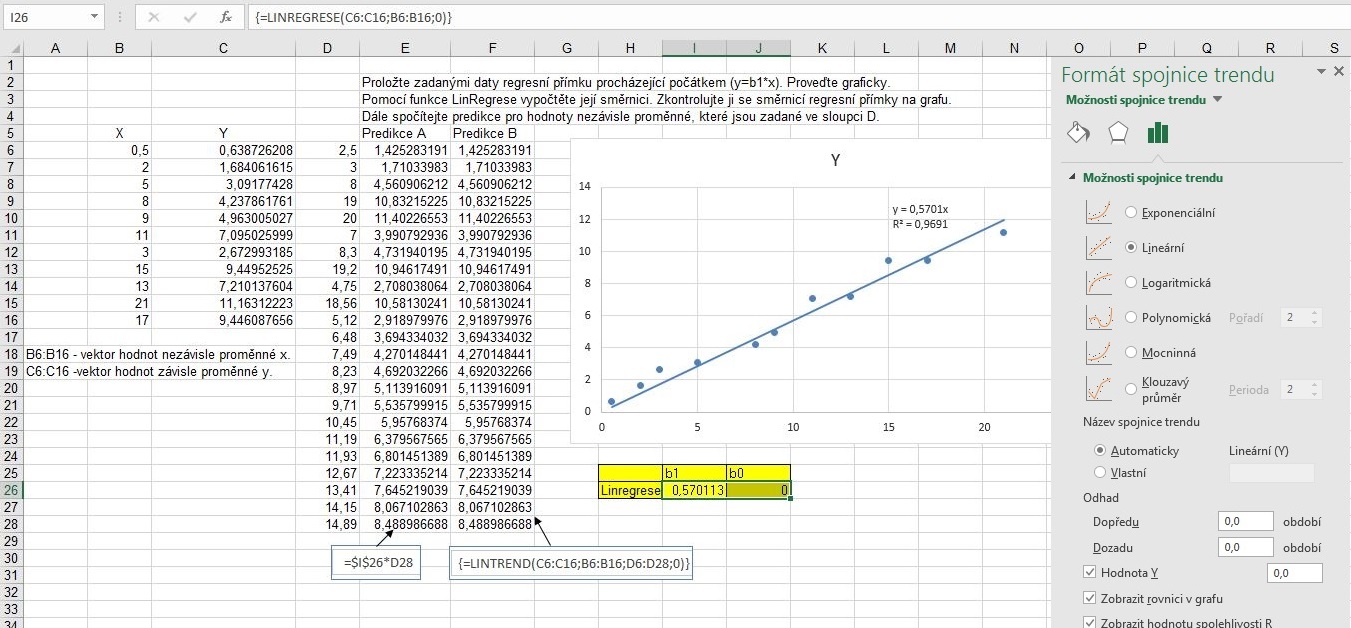
• Vyznačíme zdrojová data X,Y (následující obrázek B6:C16).
• Sestrojíme z nich bodový graf.
• Z kontextové nabídky libovolného bodu grafu volíme příkaz Přidat spojnici trendu. Objeví se okno „Formát spojnice trendu“. V něm klepneme na volbu Lineární a dále zaškrtneme volbu Hodnota Y 0,0, dále volbu Zobrazit rovnici v grafu a volitelně volbu Zobrazit hodnotu spolehlivosti R².
• Pro výpočet regresních parametrů funkcí LinRegrese() vyznačíme dvě sousední buňky v řádku (I26:J26). Tlačítkem f_x zvolíme funkci LinRegrese(). Zadáme argumenty Y a X. Za argument B zadáme hodnotu nula. Zadání ukončíme Ctrl+Shift+Enter. Parametr b₁ je první zleva, b₀=0 druhý. Příslušný vzorec vidíme na řádku vzorců.
• Hodnoty predikce počítáme z rovnice regresní funkce, či maticovou funkcí LinTrend(). Zadáme její první dva argumenty Y, X a argument B=0.

Regrese parabolou y=b₀+b₁ x+ b₂ x²

Maticová funkce LinRegrese(Y, X, B, Stat) poskytuje řádkovou matici hodnot odhadovaných parametrů.

X je matice hodnot regresorů x a x².

Y je vektor obsahující odpovídající naměřené hodnoty závisle proměnné y.

Hodnotu B nezadáváme.

Hodnotu Stat zadáme jen v tom případě, pokud bychom požadovali statistické charakteristiky regrese.

Pracovní postup (viz následující obrázek)

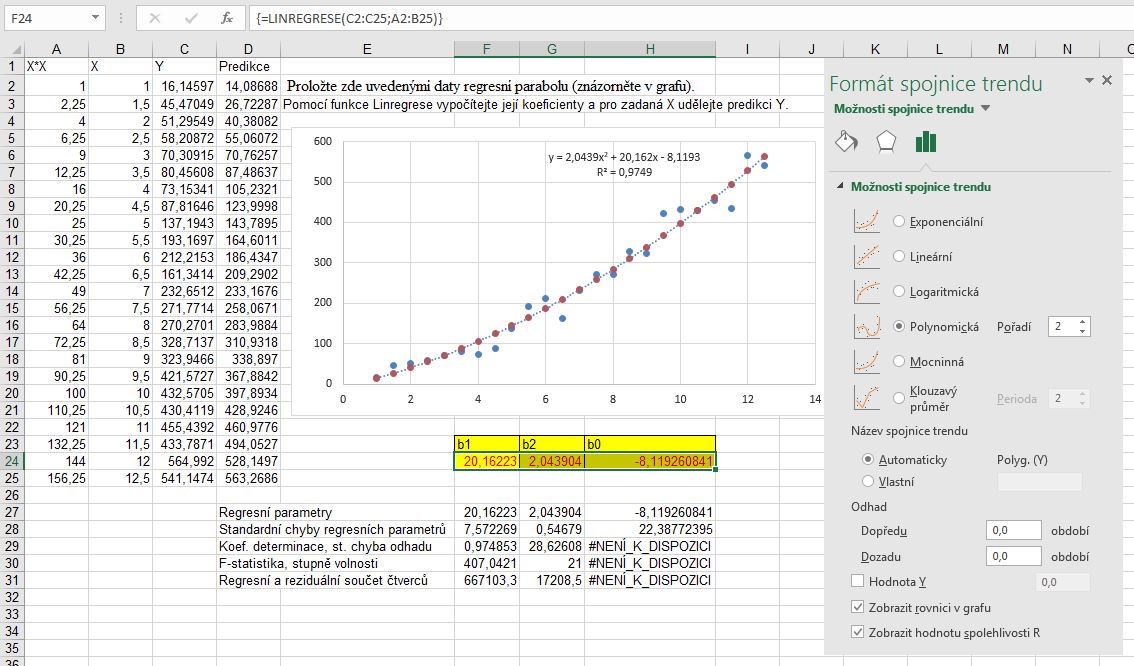
• Vyznačíme zdrojová data X,Y (předchozí obrázek B2:C25).
• Sestrojíme z nich bodový graf.
• Z kontextové nabídky libovolného bodu grafu volíme příkaz Přidat spojnici trendu. Objeví se okno „Formát spojnice trendu“. V něm klepneme na volbu Polynomická a volíme druhý stupeň polynomu (Pořadí 2). Dále volbu Zobrazit rovnici v grafu a volitelně volbu Zobrazit hodnotu spolehlivosti R².
• Nyní třeba spočítat čtverce hodnot nezávisle proměnné (do A2:A25). Pro výpočet regresních parametrů funkcí LinRegrese() vyznačíme tři sousední buňky v řádku (F24:H24). Tlačítkem f_x zvolíme funkci LinRegrese(). Zadáme argumenty Y (C2:C25) a X (A2:B25). Zadání ukončíme Ctrl+Shift+Enter. Parametr b₁ je první zleva, b₂ je druhý a b₀ je poslední. Příslušný vzorec vidíme na řádku vzorců.
• Hodnoty predikce počítáme z rovnice regresní funkce, či maticovou funkcí LinTrend() podobně jako v předchozích případech.
• Na předchozím obrázku je ještě na adrese F27:H31 výstupní matice funkce LinRegrese() pro případ hodnoty jejího argumentu Stat nastavené na TRUE. Vlevo od této matice je popis výstupních hodnot.

Exponenciální regrese

Excel též umožňuje použít regresní funkci y=b₁exp(b₂x). K určení regresních parametrů b₁ a b₂ lze použít funkci LinRegrese(), i když je regresní funkce vzhledem k druhému z nich nelineární. Pomůže nám zlogaritmování regresní funkce, čímž nelinearitu odstraníme. Dostaneme vztah ln(y)=ln(b₁)+ b₂x.

Maticová funkce LinRegrese(Y, X, B, Stat) poskytuje řádkovou matici hodnot odhadovaných parametrů.

X je sloupcová matice hodnot regresoru x.

Y je vektor obsahující odpovídající naměřené hodnoty přirozeného logaritmu závisle proměnné y.

Hodnotu B nezadáváme.

Hodnotu Stat zadáme jen v tom případě, pokud bychom požadovali statistické charakteristiky regrese.

Pracovní postup (viz následující obrázek)

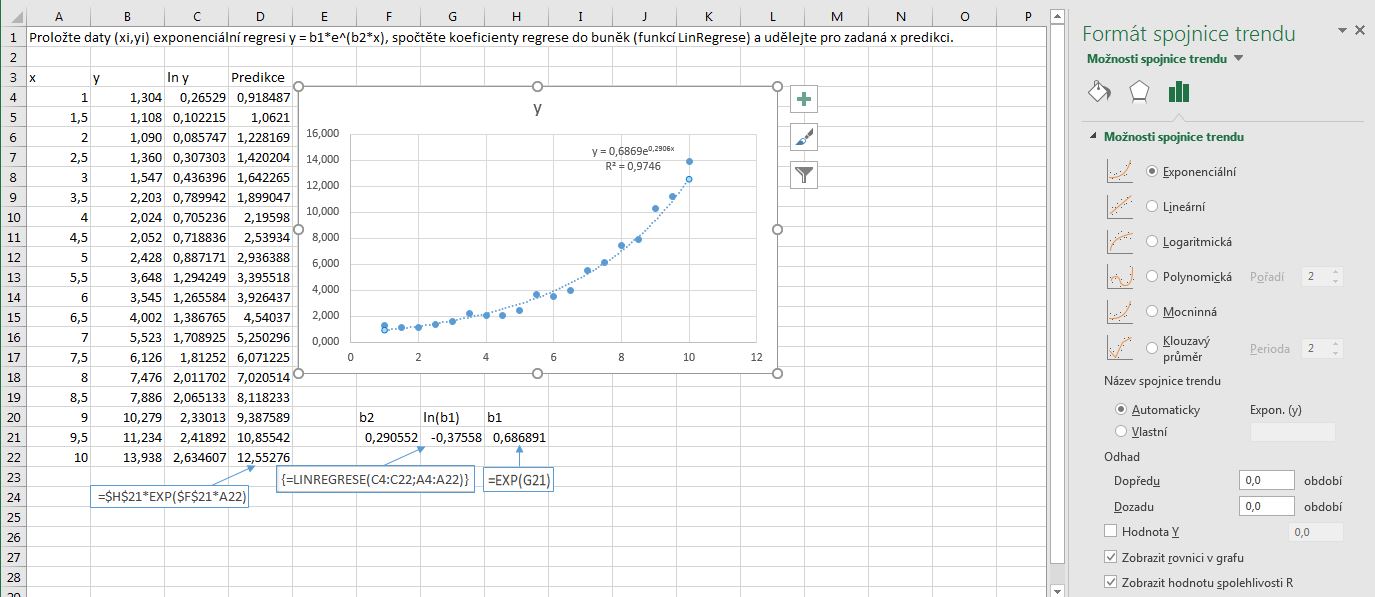
• Vyznačíme zdrojová data x, y (předchozí obrázek A4:B22).
• Sestrojíme z nich bodový graf.
• Z kontextové nabídky libovolného bodu grafu volíme příkaz Přidat spojnici trendu. Objeví se okno „Formát spojnice trendu“. V něm klepneme na volbu Exponenciální. Dále aktivujeme volbu Zobrazit rovnici v grafu a volitelně volbu Zobrazit hodnotu spolehlivosti R²x.
• Nyní spočítáme sloupec hodnot ln(Y) (C4:C22). Pro výpočet regresních parametrů funkcí LinRegrese() vyznačíme dvě sousední buňky v řádku (F21:G21). Tlačítkem f_x zvolíme funkci LinRegrese(). Zadáme argumenty ln(Y) (C4:C22) a X (A4:A22). Zadání ukončíme Ctrl+Shift+Enter. Parametr b₂ je první zleva, ln(b₁) je druhý. Hodnotu b₁ získáme odlogaritmováním (H21).
• Hodnoty predikce počítáme z rovnice regresní funkce (D4:D22).

Logaritmická regrese

Excel též umožňuje použít regresní funkci y=b₁ln(x) + b₀. K určení regresních parametrů b₁ a b₀ lze použít funkci LinRegrese().

Maticová funkce LinRegrese(Y, X, B, Stat) poskytuje řádkovou matici hodnot odhadovaných parametrů.

X je sloupcová matice hodnot přirozeného logaritmu regresoru x.

Y je vektor obsahující odpovídající naměřené hodnoty závisle proměnné y.

Hodnotu B nezadáváme.

Hodnotu Stat zadáme jen v tom případě, pokud bychom požadovali statistické charakteristiky regrese.

Pracovní postup (viz následující obrázek)

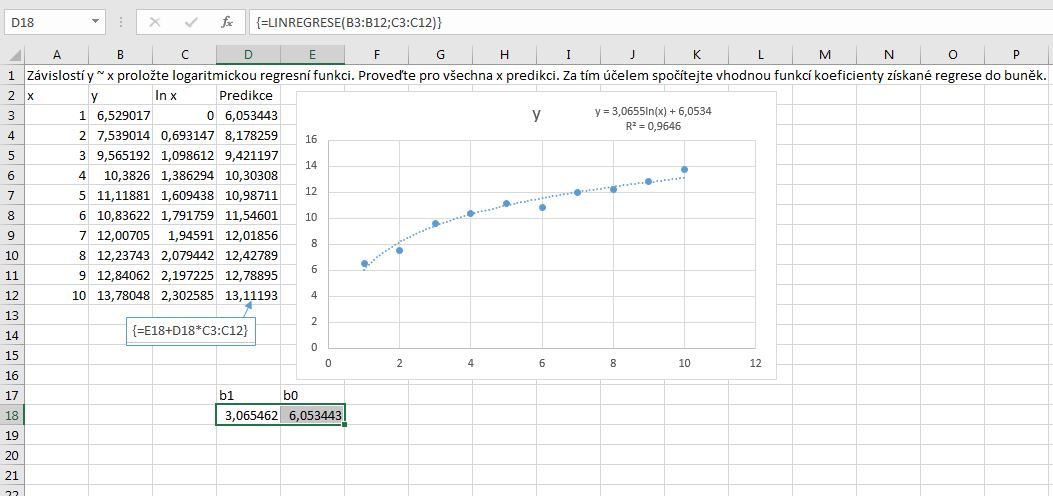
• Vyznačíme zdrojová data x, y (předchozí obrázek A2:B12).
• Sestrojíme z nich bodový graf.
• Z kontextové nabídky libovolného bodu grafu volíme příkaz Přidat spojnici trendu. Objeví se okno „Formát spojnice trendu“. V něm klepneme na volbu Logaritmická. Dále aktivujeme volbu Zobrazit rovnici v grafu a volitelně volbu Zobrazit hodnotu spolehlivosti R².
• Nyní spočítáme sloupec hodnot ln(X) (C3:C12). Pro výpočet regresních parametrů funkcí LinRegrese() vyznačíme dvě sousední buňky v řádku (D18:E18). Tlačítkem f_x zvolíme funkci LinRegrese(). Zadáme argumenty Y (B3:B12) a X (C3:C12). Zadání ukončíme Ctrl+Shift+Enter. Parametr b₁ je první zleva, b₀ je druhý.
• Hodnoty predikce počítáme z rovnice regresní funkce (D3:D12).

Mocninná regrese

Excel též umožňuje použít regresní funkci y=b₁x^b2. K určení regresních parametrů b₁ a b₂ lze použít funkci LinRegrese(), i když je regresní funkce vzhledem k druhému z nich nelineární. Pomůže nám zlogaritmování regresní funkce, čímž nelinearitu odstraníme. Dostaneme vztah ln(y)=ln(b₁)+ b₂ln(x).

Maticová funkce LinRegrese(Y, X, B, Stat) poskytuje řádkovou matici hodnot odhadovaných parametrů.

X je sloupcová matice hodnot přirozeného logaritmu regresoru x.

Y je vektor obsahující přirozený logaritmus naměřených hodnoty závisle proměnné y.

Hodnotu B nezadáváme.

Hodnotu Stat bychom zadali jen v tom případě, pokud bychom požadovali statistické charakteristiky regrese.

Pracovní postup (viz následující obrázek)

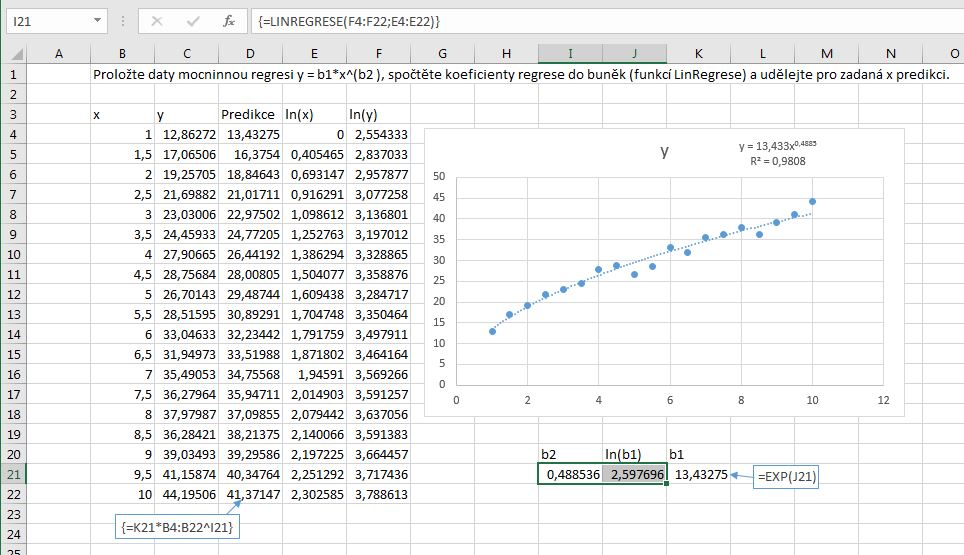
• Vyznačíme zdrojová data x, y (předchozí obrázek B4:C22).
• Sestrojíme z nich bodový graf.
• Z kontextové nabídky libovolného bodu grafu volíme příkaz Přidat spojnici trendu. Objeví se okno „Formát spojnice trendu“. V něm klepneme na volbu Mocninná. Dále aktivujeme volbu Zobrazit rovnici v grafu a volitelně volbu Zobrazit hodnotu spolehlivosti R².
• Nyní spočítáme sloupce hodnot ln(X) a ln(Y) (E4:F22). Pro výpočet regresních parametrů funkcí LinRegrese() vyznačíme dvě sousední buňky v řádku (I21:J21). Tlačítkem f_x zvolíme funkci LinRegrese(). Zadáme argumenty ln(Y) (F4:F22) a ln(X) (E4:E22). Zadání ukončíme Ctrl+Shift+Enter. Parametr b₂ je první zleva, ln(b₁) je druhý. Hodnotu b₁ získáme odlogaritmováním (K21).
• Hodnoty predikce počítáme z rovnice regresní funkce (D4:D22).