Automated area features simplification using a dissolving method
Tomas Bayer |
1. Short description of the algorithm
Area features in a map are simplified using a dissolving method. The solution is based on two phases: a plitting phace and a merging phase. During the splitting process a simplifid area is divided into small pieces. Subsequently, each piece is merged with the neighbouring area feature until nothing lefts. Dividing boundaries are formed by a skeleton. First a skeleton is constructed and converted into a planar graph (a tree). Its edges connect vertices of the simplified face. Shortest paths between nodes of all boundarinfg area features measured along the skeleton, are constructed. These sub-graphs represent dividing paths. Closing each dividing path between two nodes with a part of the boundary of the simplified area features between these nodes a new area feature is crested. It is subsequently merged with a boundaring area feature.
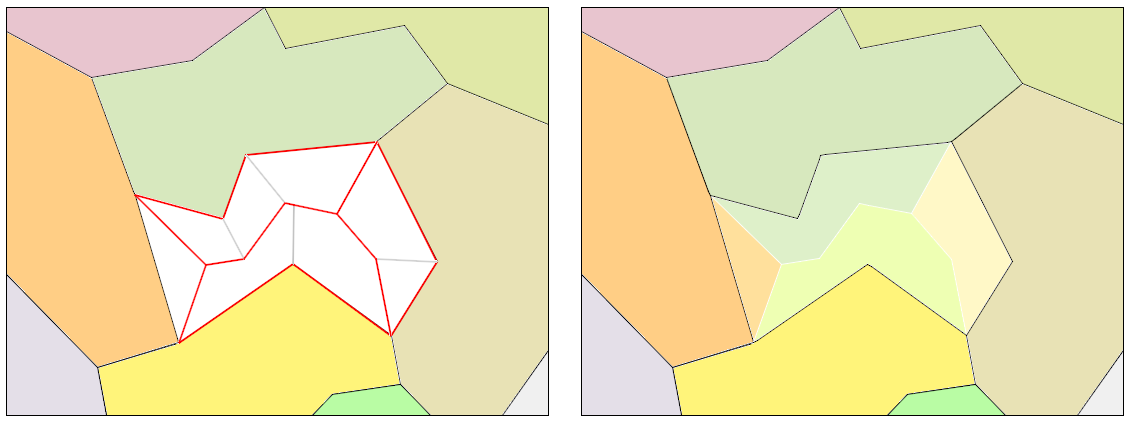
Our algoritm constructs a skeleton using a Weighted Chordal Axis. 2D Delauany triangulation is computed from the incremental method with a visibility heuristic. However, a Straight skeleton version from Marcel Sip is also available.
Cartographic results
This method is suitable for area features which are not on borders. Only the area feature which has all neighbors, can be splitted. Results are more natural compared to classical merging methods, when a simplified area feature is not dividied into pieces and its merged with some neighboring area feature at all.
2. Installation to ArcMap
Simplifying tool is written in C++ and it is compatible with ArcMap 9.x, 10.x. Do the following steps:
Start ArcMap.
Open document containing some data.
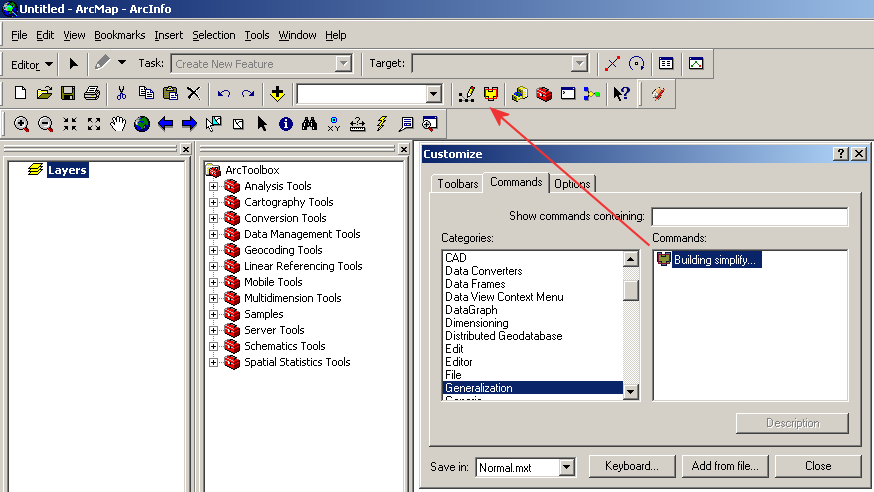
In the main menu click on Tools/Customize, tab Commands, dialog “Customize” appears.
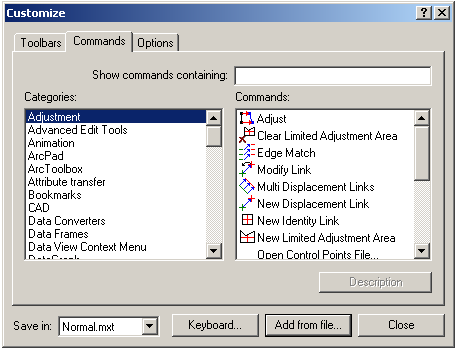
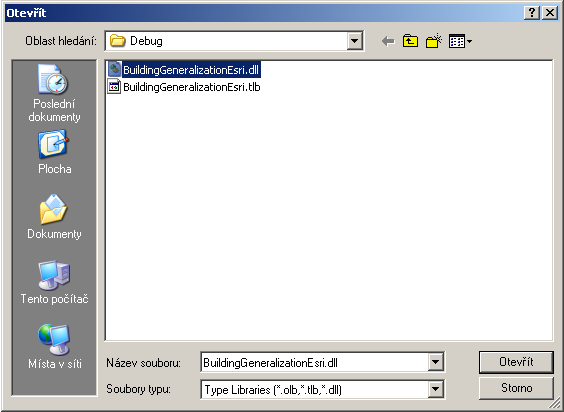
Click on the button “Add from file” and browse file “BuildingGeneralizationEsri.dll”. The new category “Generalization” will be create.
Drag the icon “Building simplify” on the main ArcMap toolbar and close the dialog.
3. Using the tool
Buildings to be simplified have to be represented by polygons. To start the simplification process do the following steps:
Using “Select Features” tool select buildings to be simplified.
Mark the layer containing buildings.
Using “Start Editing” tool allow editing of the layer.
Click on the tool and “Buildings simplify” dialog appears.
The simplification sensitivity we can regulate using track bar.
If you do not want to simplify edges containing only two points, please check the check box.
To preview the simplification process press the button “Preview”. Processing status is shown in status bar. If you are not satisfy with results, you can change the simplification sensitivity.
To apply the simplification process to data press the button “Simplify”. Processing status is shown in status bar.
Using “Save Edits” commands save results.
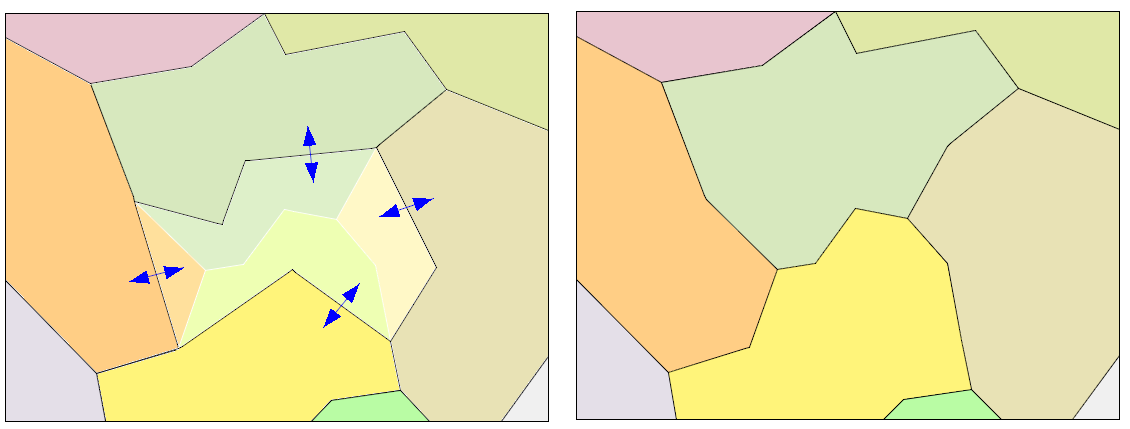
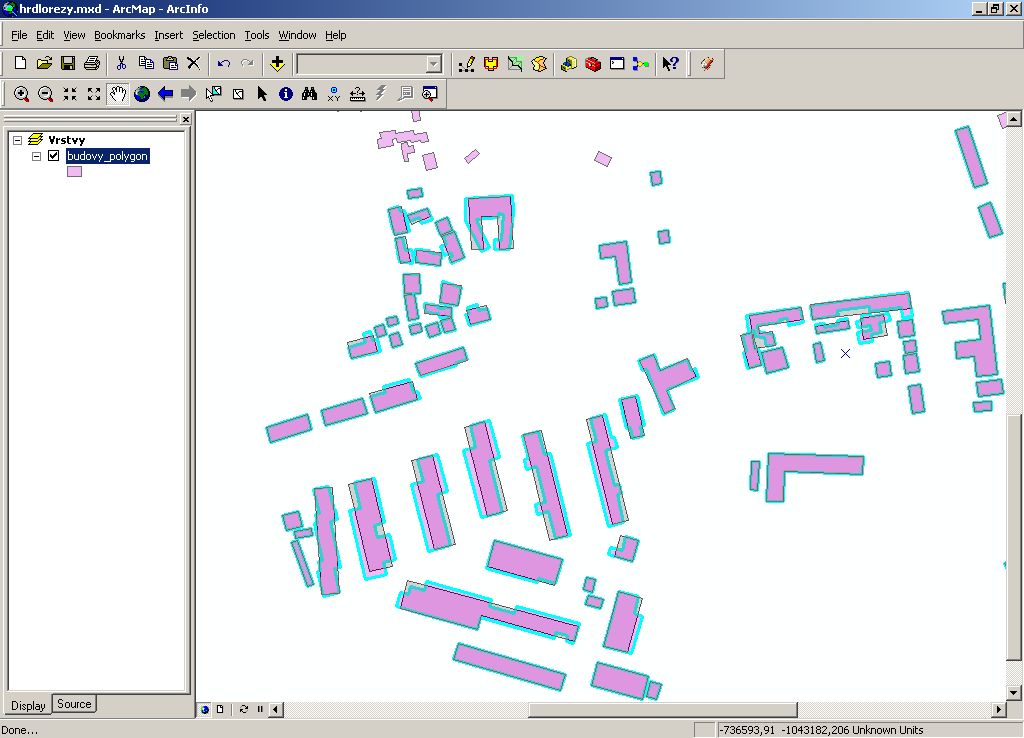
Preview to the simplification process.
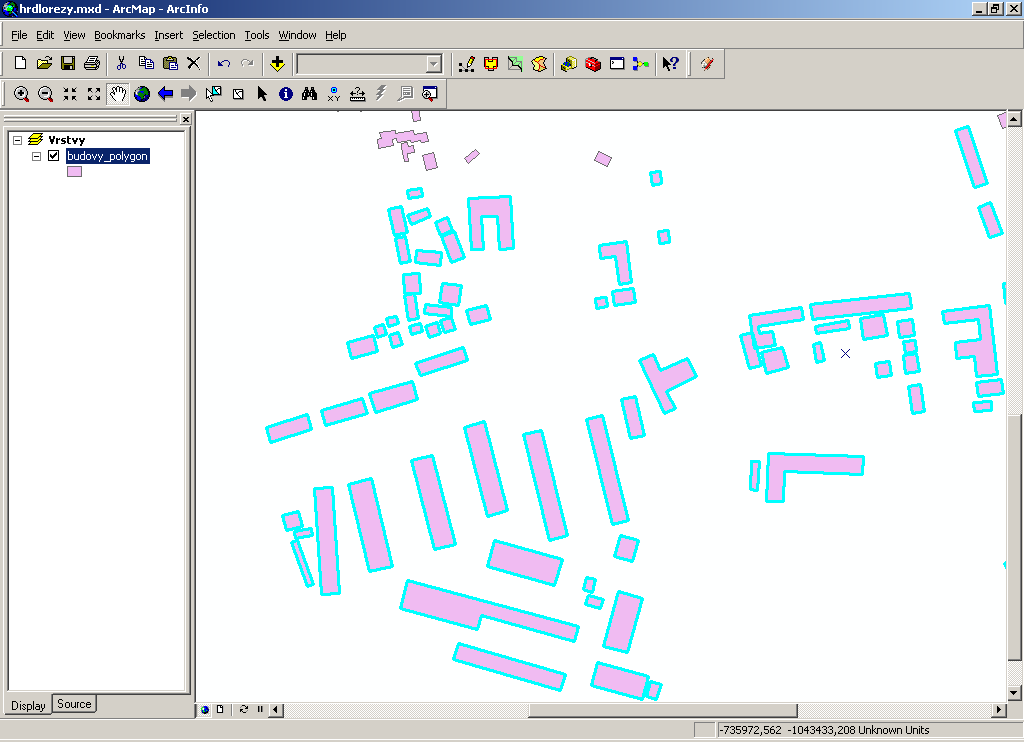
Result of the simplification process:
4. Related article
Download the article here.
5. Download
Download the software here.
Supported versions: ArcMap 9.x, 10.x.
6. References
[1] Berg M, Kreveld M, Overmars M, Schwarzkopf O (2000) Computational Geometry, Springer.
[2] Douglas D, Peucker T (1973) Algorithms for the reduction of the number of points required to represent a digitized line or its caricature, The Canadian Cartographer 10(2), pp 112-122.
[3] Dutter M. (2008) Generalization of buildings derived from high resolution remote sensing data, Wien.
[4] Freeman H, Shapira R (1975) Determining the minimum-area encasing rectangle for an arbitrary closed curve. Communications of the ACM 18 (7), pp 409-413.
[5] Galanda M (2003) Automated Polygon Generalization in a Multi Agent System, Mathematisch-naturwissenschaftlichen Fakultät, Universität Zürich.
[6] Haunert J H & Wolf A (2008) Optimal Simplification of Building Ground Plans, ISPRS Congress Beijing.
[7] Rourke O J (2005) Computational Geometry in C, Cambridge University Press, 2005.
[8] Sester M (2000) Generalization based on least square adjustment, International Archieves of Photogrammetry and Remote Sensing.
[9] Sester M, Brenner C (2004) Continuous Generalization for Visualization on Small Mobile Devices, in: Peter Fisher (Edt.): Developments in Spatial Data Handling - 11th International Symposium on Spatial Data Handling, Springer Verlag, pp 469-480.
[10] Sester M, Brenner C (2009) A vocabulary for a multiscale process description for fast transmission and continuous visualization of spatial data, Computers and Geosciences, 2009.
[11] Toussand G (1983) Solving Geometric Problems with the Rotating Calipers, McGill University Montreal.
