Automated building simplification using a recursive approach

Tomas Bayer | This email address is being protected from spambots. You need JavaScript enabled to view it.

1. Short description of the algorithm

This solution is based on the idea of hierarchical detection of vertices. Vertices are detected on the basis of their geometric significance. New vertices are gradually added to the building, among them edges of the building are geometrically reconstructed. The similar approach uses a Douglas & Peucker algorithm.

The idea of the algorithm is based on repeated search for such pairs or two pairs of points, that are locate closest to the vertices of the smallest area enclosing rectangle, constructed over every edge. Those points will represent new vertices of the building in the next step. All points Pi, which are located “between” two adjacent vertices, are matched all in all to the new edge.

Each detected edge of the buildings will be replaced by the set of new edges of simpler geometric forms. Edges of such simple geometric forms, that can not be further split, will replaced by regression lines. Neighboring detected edges are perpendicular to each other. Splitting edges will be processed using recursive approach in the same way.

Our algorithm performs recursive splitting of an edge depending on its geometric complexity and significance. The splitting criterion is calculated for each detected edge of the building. It is based on the calculation of standard deviation σ, that minimizes the sum of the squares of the points distances from the regression line; the variance of the residuals is the minimum possible. The regression line is oriented in accordance with one edge of the smallest area enclosing rectangle, it is parallel to this edge. The regression line also passes through the center of gravity of the set of points.

Cartographic results

This algorithm is suitable for stand-alone rectangular buildings. They represent buildings of “classical” geometric forms, Modern architecture is typical of the greater form variability and more complex structures. Due to the fact, that original segments of the buildings are replaced by perpendicular segments, results may look artificially. U-shaped and T-shaped buildings are in most cases well simplified. Only for buildings, where one of the edges has more complex geometric form than others, the simplification process could be made “in jump”. Such edge may be replaced by the regression line during one recursion step, which looks somewhat artificially. Our presented algorithm nearly keeps an area of the building and therefore it can be categorized in terms of the mathematical cartography as “equal area algorithm” (area distortion less than 5%).

Known issues

L-shaped and Z-shaped buildings bring more problems, an angle of rotation may not be determined correctly. As a result of the recursive splitting new vertices in such positions, which are absent in the original building, can be created. And so the resulting polygon meets geometric conditions but it is not similar to the building and it has no cartographic relevance (nor aesthetic pleasing). In general, this algorithm provides relatively good cartographic results and minimizes (for rectangular buildings) the needs of manual corrections.

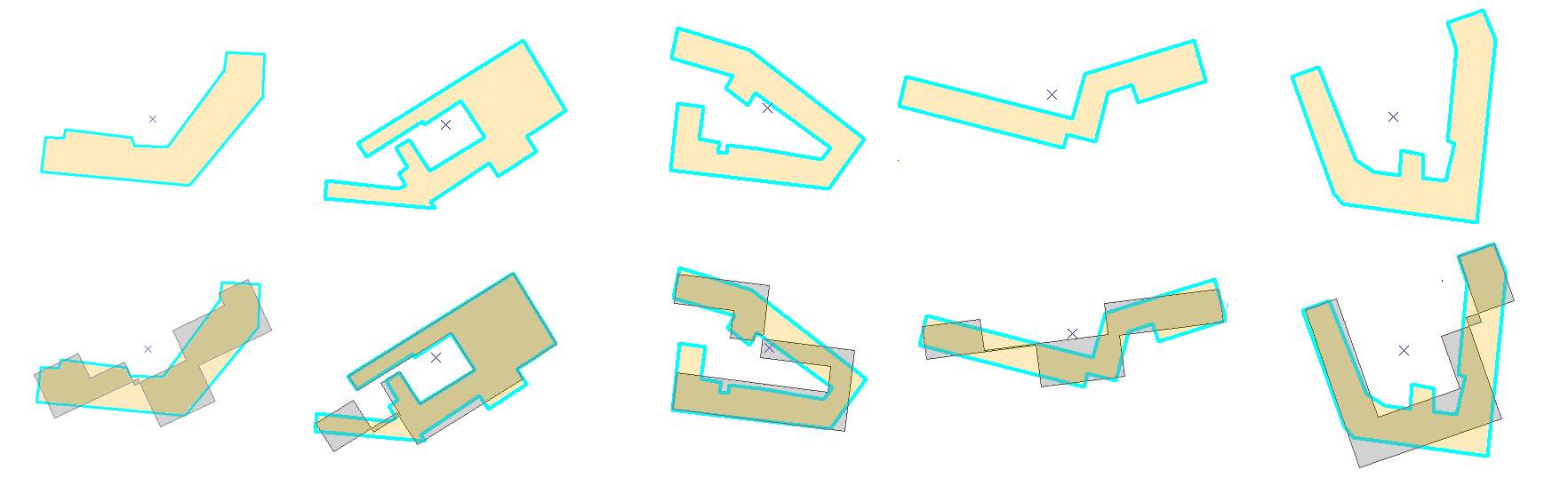
During the process of cartographic generalization we can be encountered with the problem of self intersections. They represent such situations, in which some undesirable geometric forms (long, narrow and non-rectangular buildings) as results of the generalization process have been created. Due to the topological incorrectness of such data, this error is very dangerous. Closed “pseudo region” is the result of crossing of two or more line segments. In the locus of the intersection there is no vertex inserted. Using GIS software this pseudo region will be considered as topologically incorrect.

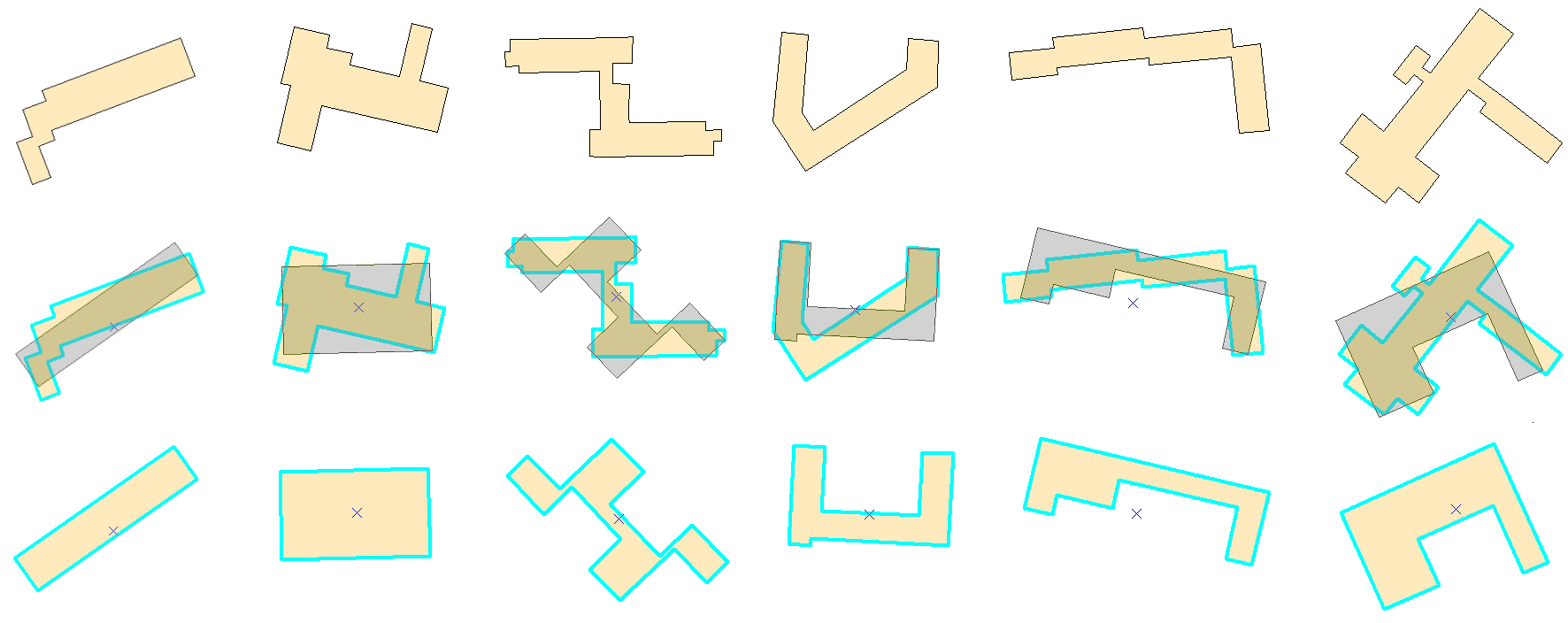
Performance

Testing was performed on the DLL version of the presented algorithm using a 2.2 GHz CPU, 2 GB RAM, OS Windows Vista and ArcGIS 9.3. Sample data set consists of 51 757 buildings with 357 516 vertices (approx. 7 vertices per building). Table 4 shows the running time depending on the amount of buildings (including redrawing all buildings and saving into feature class).

Buildings 100 200 500 1000 2000 5000 10 000 20 000 50 000
Running time [sec] 0.8 1,1 2.1 3.6 6,8 17,2 34,3 65,3 163,1

2. Installation to ArcMap

Simplifying tool is written in C++ and it is compatible with ArcMap 9.x, 10.x. Do the following steps:

1. Start ArcMap.
2. Open document containing some data.
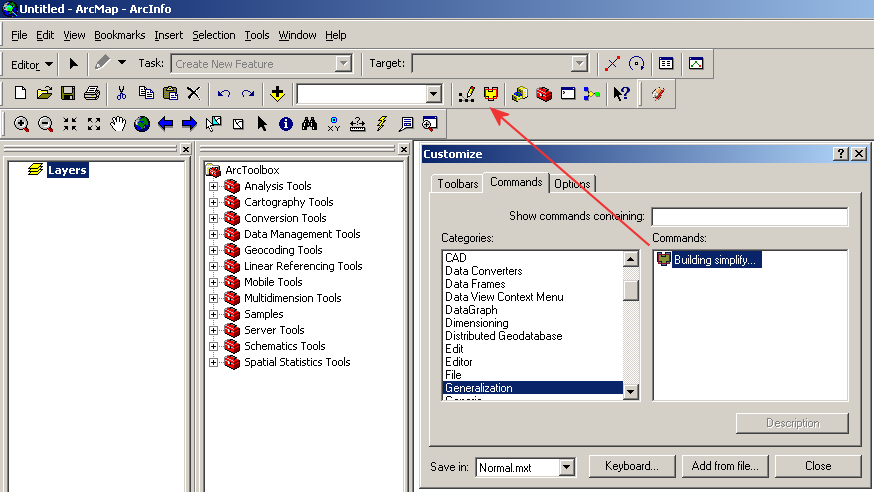
3. In the main menu click on Tools/Customize, tab Commands, dialog “Customize” appears.

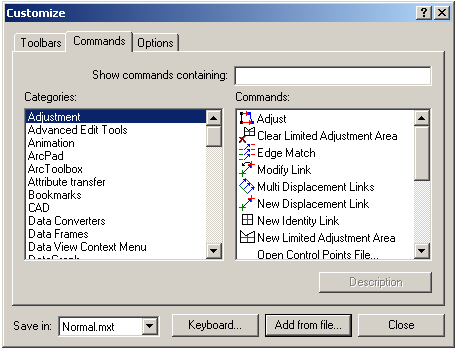
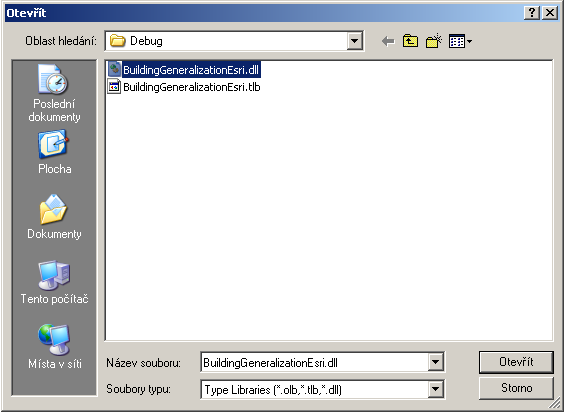
4. Click on the button “Add from file” and browse file “BuildingGeneralizationEsri.dll”. The new category “Generalization” will be create.
5. Drag the icon “Building simplify” on the main ArcMap toolbar and close the dialog.

3. Using the tool

Buildings to be simplified have to be represented by polygons. To start the simplification process do the following steps:

1. Using “Select Features” tool select buildings to be simplified.
2. Mark the layer containing buildings.
3. Using “Start Editing” tool allow editing of the layer.
4. Click on the tool and “Buildings simplify” dialog appears.
5. The simplification sensitivity we can regulate using track bar.
6. If you do not want to simplify edges containing only two points, please check the check box.
7. To preview the simplification process press the button “Preview”. Processing status is shown in status bar. If you are not satisfy with results, you can change the simplification sensitivity.
8. To apply the simplification process to data press the button “Simplify”. Processing status is shown in status bar.
9. Using “Save Edits” commands save results.

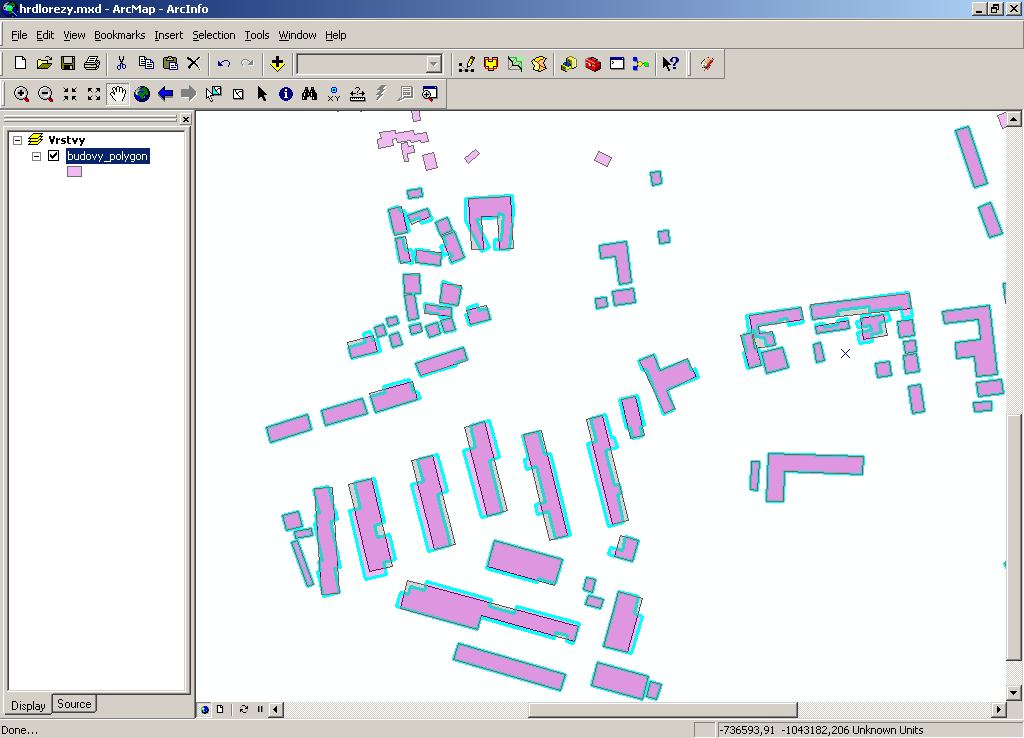
Preview to the simplification process.

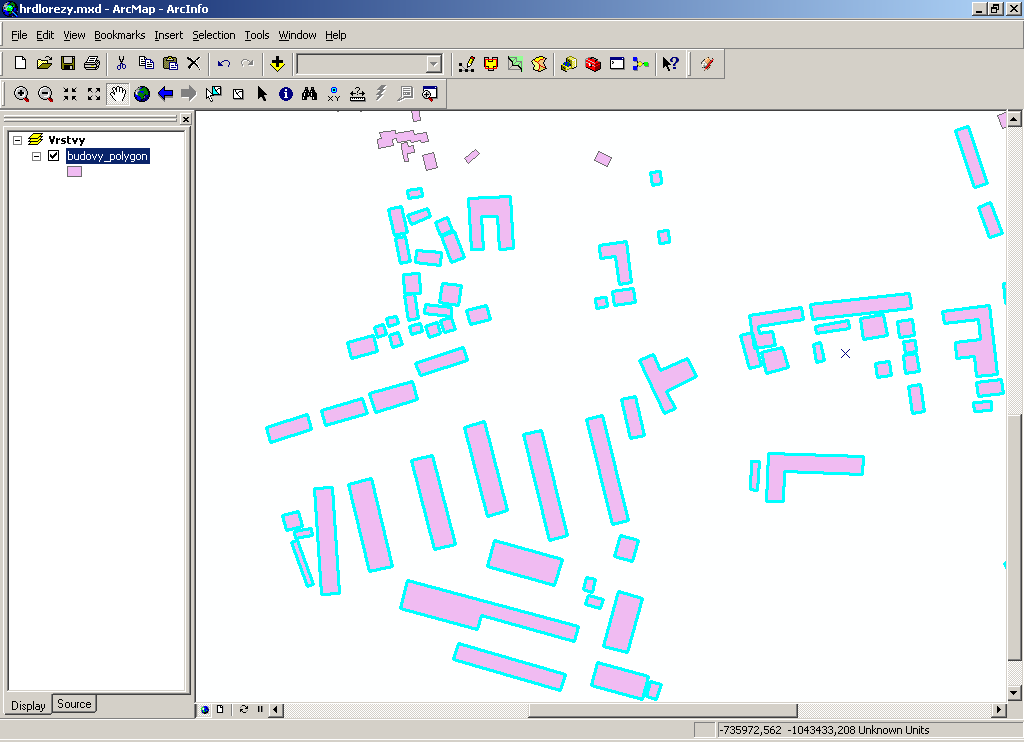
Result of the simplification process:

4. Related article

Download the article here.

5. Download software

Download the software here. The source code (C++) is available at Github. ArcGIS runtime Qt SDK C++ API is required.

Supported versions: ArcMap 10.x.

6. References

[1] Berg M, Kreveld M, Overmars M, Schwarzkopf O (2000) Computational Geometry, Springer.

[2] Douglas D, Peucker T (1973) Algorithms for the reduction of the number of points required to represent a digitized line or its caricature, The Canadian Cartographer 10(2), pp 112-122.

[3] Dutter M. (2008) Generalization of buildings derived from high resolution remote sensing data, Wien.

[4] Freeman H, Shapira R (1975) Determining the minimum-area encasing rectangle for an arbitrary closed curve. Communications of the ACM 18 (7), pp 409-413.

[5] Galanda M (2003) Automated Polygon Generalization in a Multi Agent System, Mathematisch-naturwissenschaftlichen Fakultät, Universität Zürich.

[6] Haunert J H & Wolf A (2008) Optimal Simplification of Building Ground Plans, ISPRS Congress Beijing.

[7] Rourke O J (2005) Computational Geometry in C, Cambridge University Press, 2005.

[8] Sester M (2000) Generalization based on least square adjustment, International Archieves of Photogrammetry and Remote Sensing.

[9] Sester M, Brenner C (2004) Continuous Generalization for Visualization on Small Mobile Devices, in: Peter Fisher (Edt.): Developments in Spatial Data Handling - 11th International Symposium on Spatial Data Handling, Springer Verlag, pp 469-480.

[10] Sester M, Brenner C (2009) A vocabulary for a multiscale process description for fast transmission and continuous visualization of spatial data, Computers and Geosciences, 2009.

[11] Toussand G (1983) Solving Geometric Problems with the Rotating Calipers, McGill University Montreal.